H4: Het wereldbeeld

H4.1 Het astronomische wereldbeeld

Het is in onze cultuur gebruikelijk om alle verworvenheden van de natuurwetenschappen toe te schrijven aan lieden als Copernicus (1473-1543), Dalton (1766-1844) en Darwin (1809-1882), maar twee millennia eerder werd er in Griekenland al gediscussieerd over het zonnestelsel, atomen en de evolutie van het leven. Hoewel het de vraag is of die zaken allemaal van puur Griekse oorsprong waren, en niet gestolen van hun aartsvijanden – de Perzen –, gaan we er bij gebrek aan kennis daarover maar even van uit dat de bewondering voor de Griekse oudheid terecht is en dat zaken als wijsbegeerte, logica en natuurwetenschap bloemen van Griekse bodem zijn. Toch moeten we met dat soort opvattingen voorzichtig zijn. De bewering dat de Grieken de ‘uitvinders’ van de democratie zijn is bijvoorbeeld onjuist. Weliswaar hebben de Atheners enige tijd ook het minder belangrijke deel van de mannelijke bevolking laten meespelen, maar de manier waarop de Grieken normaal gesproken hun staatszaken regelden zouden wij allerminst democratisch noemen. Die opvatting van een Griekse ‘democratie’ is misschien ontstaan doordat dat woord van oorsprong Grieks is, maar het gezamenlijk besturen van een stad of landstreek door de welgestelde inwoners ervan is de oudste regeringsvorm die de mens kent en heeft niet speciaal iets met Grieken te maken. In het Griekenland van toen ging het er trouwens helemaal niet zo wijs, logisch en democratisch aan toe. Denk aan Sokrates, die tot de gifbeker werd veroordeeld omdat hij lastige vragen stelde. En toen Aristarchos van Samos (ca. 310-230 v.Chr) ongeveer hetzelfde bedacht als Copernicus achttien eeuwen later, overkwam hem ook hetzelfde als diens voorvechter Galilei (1564-1642). Hij moest zijn wereldbeeld afzweren omdat hem een proces wegens godslastering boven het hoofd hing¹. Er was bij het proces van Galilei in 1633 dus niets nieuws onder de mediterrane zon.

Volgens Archimedes (287-212 v.Chr.) was Aristarchos² van mening dat de vaste sterren en de zon onbeweeglijk waren, en dat de aarde in een cirkelvormige baan om de zon wentelde, waarbij de zon in het middelpunt van die baan stond. Uit het feit dat er ondanks die rondwentelende aarde zichtbaar niets aan de sterrenhemel veranderde concludeerde Aristarchos dat de sterren zeer ver weg moesten staan. Hoe kwam hij op de gedachte dat de aarde om de zon draaide? Waarschijnlijk doordat hij er achter kwam dat de zon veel groter moest zijn dan de aarde. Hij bedacht namelijk een methode om de afstand tot de zon te bepalen.

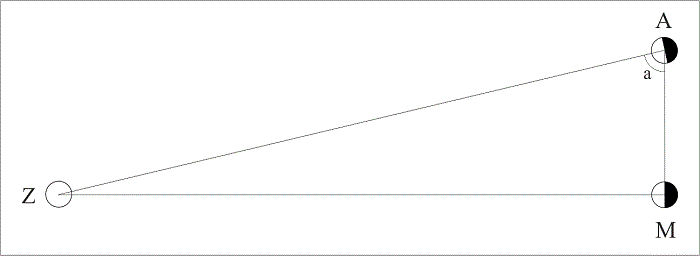
Afbeelding H4.1.1. Als iemand op aarde (A) de halve maan (M) ziet, dan betekent dat, dat de lijn (AM) tussen die persoon en de maan (M) loodrecht staat op de lijn tussen de zon (Z) en de maan (ZM). Door hoek a te meten kan de verhouding tussen AZ en AM vastgesteld worden. Goniometrische tabellen bestonden er in de tijd van Aristarchos nog niet, net zo min als theodolieten. Het eerste resultaat was dan ook niet erg correct. Blijkbaar stelde Aristarchos vast dat hoek a ongeveer 87° bedroeg. Dat betekent dat de verhouding van de lengte van de lijnen AM en AZ ongeveer één op negentien is³. De zon stond dus ongeveer negentien keer zo ver weg als de maan. Nu lijkt de maan aan de hemel bijna net zo groot als de zon, hetgeen bij een volledige zonsverduistering mooi te controleren is. De conclusie van Aristarchos was dat de werkelijke diameter van de zon dan ook negentien keer zo groot moest zijn als die van de maan.

Verder wist hij dat bij een maansverduistering de diameter van de schaduwkegel van de aarde groter is dan de diameter van de maan. Hij schatte die schaduwkegel ongeveer 2¾ maal zo groot⁴. Omdat de zon zo ver weg staat mag aangenomen worden dat de diameter van die schaduwkegel nauwelijks kleiner is dan de diameter van de aarde zelf. Dat zou dus betekenen dat de aarde een 2¾ maal zo grote diameter heeft dan de maan. Voor de negentien maal verder weg staande zon betekent dat dus dat de diameter daarvan ca. 19 / 2¾ = 6,9 maal zo groot is als die van de aarde. Daarna ligt het voor de hand om aan te nemen dat het kleinere lichaam (aarde) om het grotere (zon) heen draait. Zonder ook maar enig idee te hebben van de ware verhoudingen kon Aristarchos zo tot een modern heliocentrisch wereldbeeld komen. Toch kon hij niet meer doen dan de relatieve afmetingen van de hemellichamen berekenen. Het één was zoveel maal groter dan het ander, maar van de absolute afmetingen had hij geen idee. Wat hem ontbrak was een meetlat van het juiste formaat.

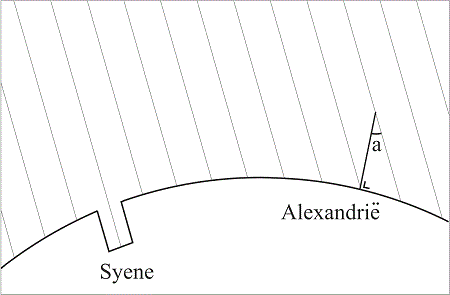
Afbeelding H4.1.2. Die werd bedacht door Erathostenes van Kyrene (ca. 276-194 v.Chr.). Erathostenes wist dat er in Zuid-Egypte, bij Syene, een diepe put was waarin de zon op de langste dag aan het begin van de zomer, op het middaguur loodrecht naar beneden scheen. Ook kende hij de afstand van Syene naar Alexandrië: 5250 stadiën. Als hij op de langste dag in Alexandrië een loodrechte staaf oprichtte, dan wierp die op het middaguur een schaduw die 7½° uit het lood stond (op afbeelding H4.1.2. hoek a). Daaruit trok Erathostenes de conclusie dat de aardomtrek 360 / 7½ = 48 keer zo groot was als de afstand van Syene naar Alexandrië. Zo kwam hij op 252.000 stadiën. Rekenen we stadiën van 185 meter, dan bedroeg de aardomtrek volgens hem dus 46.620 kilometer (de werkelijke waarde is 40.000 km). Er van uitgaande dat de omtrek van een cirkel ongeveer ²²/7 maal zo groot is als de diameter ervan, dan komt die diameter op ca. 80.000 stadiën. Eindelijk was er een meetlat waarmee de hemel gemeten kon worden.

Op de methode van Erathostenes is tweeduizend jaar later veel kritiek gekomen. Syene ligt niet precies ten zuiden van Alexandrië, de beroemde put lag niet precies op de Kreeftskeerkring, de hoek in Alexandrië was niet precies 7½°, de afstand tussen Syene en Alexandrië was niet precies 5250 stadiën, kortom Erathostenes zou een goed resultaat hebben behaald doordat allerlei fouten elkaar toevallig ophieven. Een mens moet een beetje geluk hebben. Met behulp van deze meetlat kregen onze voorouders in ieder geval een indruk van de werkelijke verhoudingen in het systeem zon – aarde – maan. En een indruk van de onbevattelijke uitgestrektheid van de wereld daarbuiten.

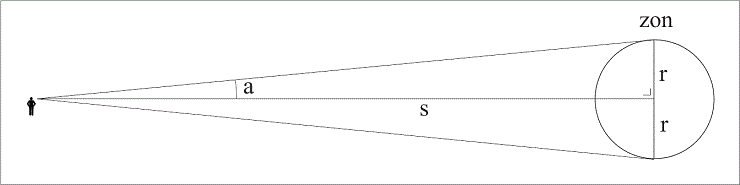
Afbeelding H4.1.3. Voortbordurend op de resultaten van Aristarchos betekent het dat de diameter van de maan ca. 29.000 stadiën zou bedragen, en die van de zon ca. 554.000. Hoe valt daaruit de afstand naar die hemellichamen te bepalen? Aan de hemel doet de zon (en de maan) zich aan ons voor als een schijf van ongeveer een halve graad (30’). Dat betekent dat hoek a (afbeelding H4.1.3.) ongeveer 15’ bedraagt. Bij zo’n hoek verhouden de lijnstukken s (afstand naar de zon) en r (straal van de zon) zich ongeveer als 230 : 1. De afstand naar de zon zou dus ca. 230 maal de halve diameter van de zon bedragen, ofwel ca. 64.000.000 stadiën. Een kleine twaalf miljoen kilometer. Dat is slechts 8% van de werkelijke waarde, maar voor mensen die meer dan 2000 jaar geleden leefden moet het een duizelingwekkend getal zijn geweest. In werkelijkheid is de aarde niet 2³/4 keer zo groot als de maan, maar ongeveer 3²/3. En staat de zon niet 19 keer zo ver weg, maar ongeveer 400 keer. En de hoek waaronder we de zon zien is wat groter dan een halve graad, zodat de verhouding tussen r en s (op afbeelding H4.1.3.) ongeveer 1 : 215 is. De diameter van de zon is niet, zoals Aristarchos dacht, ongeveer zeven keer groter dan die van de aarde, maar meer dan honderd keer. Dat betekent dat er meer dan een miljoen aardbollen in de zon passen. Men spreekt dus wel terecht van een “lekker zonnetje”.

In de tijd van Plinius de Oudere (ca. 23-79) konden hoekmetingen blijkbaar al zeer nauwkeurig uitgevoerd worden. Plinius schat de afstand van de aarde naar de maan op 2.000.000 stadiën (ca. 97% van de werkelijke waarde) en de afstand van de aarde naar de zon op 500.000.000 stadiën (ca. 62% van de werkelijke waarde)⁵. Dat betekent dat de zon volgens hem 250 keer zo ver weg stond als de maan. En dat wil zeggen dat de hoek zon – aarde – maan bij halve maan op ca. 89°46’ werd geschat. De werkelijke waarde ligt in de buurt van 89°51’. Een meting in de tijd van Plinius week dus slechts 5’ af van een moderne meting! Het twaalfde deel van een graad! Zou dat, net zoals bij Erathostenes, meer geluk dan wijsheid zijn geweest? Er is nóg een bron die suggereert dat men in de oudheid hoeken tot op een twaalfde graad nauwkeurig kon meten.

H4.2 Het geografisch wereldbeeld

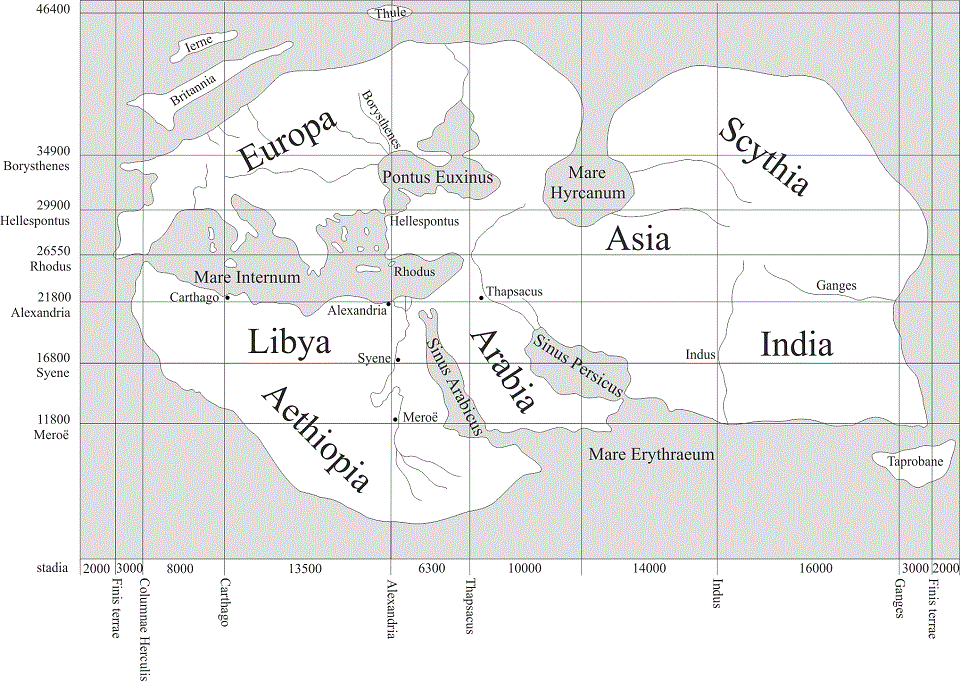
Afbeelding H4.2.1. Ook in de Geographia van Ptolemaeus (87-150) wordt een nauwkeurigheid van een twaalfde graad gehanteerd. Want dat is het verschil tussen 1/6° en 1/4°, twee breuken die in het geschrift van Ptolemaeus veel voorkomen. Daarmee is echter niet gezegd dat de opgaven van Ptolemaeus ook nauwkeurig zijn. Maar voordat we Ptolemaeus onder de loupe nemen werpen we even een blik op het aardrijkskundige beeld dat men in de eerste eeuwen van onze jaartelling van de wereld had. De bekende wereld was toen ongeveer net zo groot als op de Peutinger-kaart. Van west naar oost lag ze tussen de Atlantische Oceaan en de Golf van Bengalen, waar de Ganges in uitmondt. Van noord naar zuid was de situatie onduidelijker. Noord-Europa en het Russisch Laagland waren onbekend terrein. Van Afrika kende men slechts het noorden. Alleen in Egypte en Arabië strekte de bekende wereld zich verder zuidwaarts uit. Tussen 500 v.Chr. en 1500 n.Chr. is er (in Europa) aan dit wereldbeeld nauwelijks iets veranderd.

Op kaartje H4.2.1 is de wereld volgens Erathostenes⁶ afgebeeld. Het werelddeel ten zuiden van Europa heeft daar nog de oude Griekse naam Libya. Drie eeuwen later zouden Strabo⁷ (ca. 64 v.Chr-19 n.Chr.) en Pomponius Mela⁸ (eerste helft 1e eeuw) de wereld nog op precies dezelfde wijze beschrijven, behalve dan dat Libya in hun tijd Afrika heette, de naam die de Romeinen er aan gaven. Zelfs van dit eenvoudige wereldbeeld was een groot deel verzonnen. Zo heeft men eeuwen lang gedacht dat de Kaspische Zee (Mare Hyrcanum) in verbinding stond met de Arctische Oceaan.

Alleen de landen rond de Middellandse Zee behoorden tot het echt bekende terrein. Naar het oosten toe had de Perzische koning Darius I in de zesde eeuw v.Chr. gebied veroverd tot aan de Indus. Dank zij de Griekse ontdekkingsreiziger Scylax van Caryanda raakte dat deel van de wereld toen beter bekend. En natuurlijk ook door de verovering van het Perzische rijk door Alexander de Grote (356-323 v.Chr.). Er was ook eigenlijk wel meer aardrijkskundige kennis, maar men hechtte daar niet altijd geloof aan. Het was voor onze verre voorouders ook onmogelijk om onderscheid te maken tussen werkelijkheid en verzinsel. Over de herkomst van twee stoffen die tot ca. 500 v.Chr. zeer kostbaar waren, barnsteen en tin, zegt Herodotus (ca. 485 – na 430 v.Chr.) bijvoorbeeld het volgende⁹:

Herodotus weet niet waar de genoemde rivier en eilanden liggen, dus gelooft hij er niet in. Hij weet alleen dat beide producten van zeer ver komen. Wij weten nu dat tin in de tijd van Herodotus uit Bretagne en Zuid-Engeland kwam en Barnsteen uit Jutland en Sleeswijk-Holstein. Misschien zelfs uit Noord-Nederland¹⁰. Dat waren streken die voor een Griek uit de vijfde eeuw v.Chr. echter ver buiten de horizon lagen.

Pas ruim een eeuw(?) later zou een andere Griek uit de kolonie Masillia (Marseille) een tocht over de oceaan wagen om de herkomst van tin en barnsteen te achterhalen. Het is deze Griek, Pitheas, die in een ca. 320 v.Chr. geschreven boek voor het eerst het eiland Thule noemt, dat in het uiterste noorden zou liggen (zie afbeelding H2.3.6). Vandaar dat Thule te vinden is op de kaart van Erathostenes (afbeelding H4.2.1.), die op zijn beurt weer ruim een eeuw(?) ná Pitheas leefde. Men ziet in Taprobane (onder India) wel Sri Lanka (Ceylon, Serendib), maar het is mogelijk slechts een verzonnen land, net als Utopia.

Het is voor ons heel logisch om Europa, Azië en Afrika als een samenhangende landmassa te zien, die geheel door zeeën is omgeven, maar in de oudheid was men daar helemaal niet zo zeker van. Wij weten dat er een Noordelijke IJszee is, maar in de oudheid wist niemand daarvan. Op grond van de wetenschap dat de aarde een bol was nam men aan dat een westkust ook logischerwijs een oostkust inhield. Sinds ca. 600 v.Chr. bestond het vermoeden dat de continenten ook aan de zuidzijde door zee werden begrensd, dus nam men dan ook maar een noordelijke kust aan. Wij leerden op school dat Vasco da Gama (1469-1524) de eerste was die rond Afrika voer, maar Herodotus weet ons te vertellen dat dit kunststukje reeds onder de Egyptische farao Necho (regeerde 609-595 v. Chr.) werd uitgevoerd¹¹:

Phoinikiërs zijn Foeniciërs, beroemde zeevaarders uit de oudheid, en ‘Zuilen van Hèraklès’ is een poëtische benaming van de Straat van Gibaltar. De Foeniciërs van koning Necho deden het rondje Afrika dus andersom dan Vasco da Gama. Ze voeren weg vanuit de Rode zee en kwamen door de Middellandse Zee weer terug. Merk op dat Necho bezig was met een kanaal tussen de Nijl en de Rode Zee, zodat er een verbinding met de Middellandse Zee zou ontstaan. Dat kanaal zou echter pas onder de Perzische koning Darius (522-485 v.Chr.) in 518 v.Chr. worden voltooid¹². Het had wel hetzelfde doel, maar niet hetzelfde verloop als het in 1869 opengestelde Suezkanaal. Herodotus kon niet geloven dat de Foeniciërs bij het omvaren van Afrika de zon aan de rechterkant hadden, maar dat is nu juist een sterke aanwijzing dat de expeditie werkelijk heeft plaatsgevonden. Herodotus is trouwens niet de enige die van een dergelijke tocht melding maakt. Waar Pomponius Mela de Aethiopes van het land Meroë beschrijft (zie de kaart van Erathostenes, afbeelding H4.2.1.) zegt hij op een gegeven moment (Chorographia III, 89/90)¹³:

De richting van de Eurus (twaalfwindensysteem) wordt gevolgd in de Rode Zee. Hanno de Cathager staat ook bekend als Hanno de Zeevaarder. De grootouders van Pomponius Mela leefden in de eerste eeuw v.Chr. Gades is Cadiz in Zuid-Spanje. Als Ptolemaeus deze teksten had gekend, dan had hij zijn wereldkaart (afbeelding H4.3.1.)¹⁴ wellicht anders getekend. Want Ptolemaeus dacht inderdaad dat het landmassief in een grote boog om de Indische oceaan heen lag en ver in het oosten weer op Azië aansloot.

H4.3 Ptolemaeus

In tekst H4.2 noemde Pomponius Mela drie theorieën over de vorm van Afrika en de uitgestrektheid van de Indische Oceaan:

Blijkbaar zijn er in de oudheid minstens drie pogingen gedaan om rond Afrika te varen. Herodotus noemt een succesvolle poging rond 600 v.Chr., waarbij de tocht van de Rode Zee naar de Middellandse Zee ging. En Pomponius Mela noemt een vanwege voedselgebrek mislukte poging van Hanno de Carthager (ca. 450 v.Chr.), die vanuit de Middellandse Zee vertrok, en een zekere Eudoxus die in de eerste eeuw v.Chr. vanuit de Rode Zee naar Cadiz voer. Bovendien namen alle Griekse aardrijkskundigen aan dat de drie toen bekende continenten door een oceaan omgeven werden, zodat men aan welke kant van de wereld dan ook op een gegeven moment op water moest stuiten. Afbeelding H4.3.1.

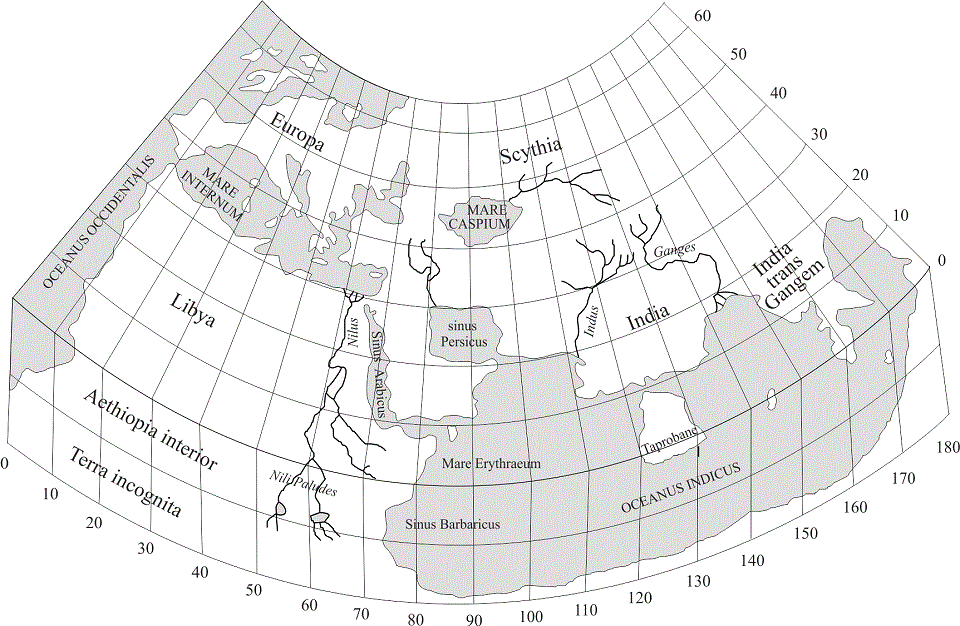
Van Ptolemaeus krijgen we echter een ander wereldbeeld. De Indische Oceaan is een binnenzee en het vaste land is aan de noord- en zuidzijde niet begrensd. Eventuele zeeën vallen buiten zijn kaart. Of dacht hij tevens dat Afrika zich eindeloos uitstrekte en tenslotte weer op Europa aansloot? Hij tekent wel een westkust, maar de daaruit logischerwijs voortvloeiende oostkust ligt blijkbaar ook buiten het afgebeelde deel van de wereld.

Ptolemaeus was dus een aanhanger van de eerste door Pomponius Mela genoemde theorie, en diens opmerking dat de kusten van Afrika enigszins bekend waren gold blijkbaar niet voor iedereen. De werken van Herodotus en Mela waren blijkbaar geen gemeengoed. Of ze werden niet door iedereen geloofd. Verder is er nog iets merkwaardigs aan de wereldkaart van Ptolemaeus. Hij laat zijn lengtegraden veel te snel oplopen. Ze zijn slechts ongeveer ²/3 van hun werkelijke waarde. Omdat Ptolemaeus de wereld wel degelijk als een bol beschouwde moeten we eigenlijk zeggen dat hij de afstanden langs de lengtegraden overschatte. Ze zijn bij hem 1½ keer groter dan in werkelijkheid. Dit feit is één van de aanwijzingen dat het werk van Ptolemaeus niet berustte op metingen, ervaringen, of studie, maar op het klakkeloos overnemen van bepaalde opvattingen en verder vlijtig kopieerwerk. Dat hij als de grootste aardrijkskundige van de oudheid wordt beschouwd dankt hij hoofdzakelijk aan de roem die hij in de 15e eeuw in Europa verwierf.

Omdat de oudste uitgave van het werk van Ptolemaeus geen kaarten bevat rijst altijd weer de vraag of men zulke documenten in de oudheid wel had. Het antwoord is natuurlijk ‘ja’. Wie de continenten en hun vormen wil beschrijven heeft daar een plaatje bij nodig. Ongetwijfeld hebben Erathostenes, Strabo en Mela de wereld op een stuk papier getekend voordat ze aan het beschrijven sloegen. Het werk van Ptolemaeus is zelfs niets anders dan een verzameling aanwijzingen voor het kopiëren van kaarten. Namelijk van de kaarten waar Ptolemaeus zelf over beschikte en die hij wellicht zelf had getekend. De beste manier was om aan alle belangrijke punten op die kaarten coördinaten toe te kennen en daar lijsten van te maken. Zodoende kan men die kaarten nu opnieuw ‘plotten’. En zodoende kunnen wij nu ook zien dat de manier om moderne topografische kaarten te maken niet een ‘wedergeboorte’ is van methoden uit de oudheid, maar echt een uitvinding uit de 16e eeuw.

In verband daarmee valt altijd de naam Gemma Frisius (1508 – 1555), die in het dagelijks leven Jemme Reinersz heette, afkomstig uit Dokkum. In een boekje uit 1537 beschrijft Frisius hoe met behulp van een meetbord (planchet), een kompas en een meetketting de onderlinge afstand en richting van plaatsen vastgesteld kan worden¹⁵. Vanaf dat moment trekken landmeters, zoals de bekende Jacob van Deventer (ca. 1505-1575) het land in om er nauwkeurige kaarten van te gaan vervaardigen. “Dat moment” is ruwweg 1550. Het is in ieder geval zeker dat kaarten die vóór het midden van de zestiende eeuw zijn gepubliceerd niet berusten op wiskundige landmeting, maar op schetsen die werden gemaakt door mensen die de betreffende landstreken bereisd hadden en er misschien met behulp van een kompas of astrolabium en het schatten van afgelegde afstanden waarnemingen hadden gedaan.

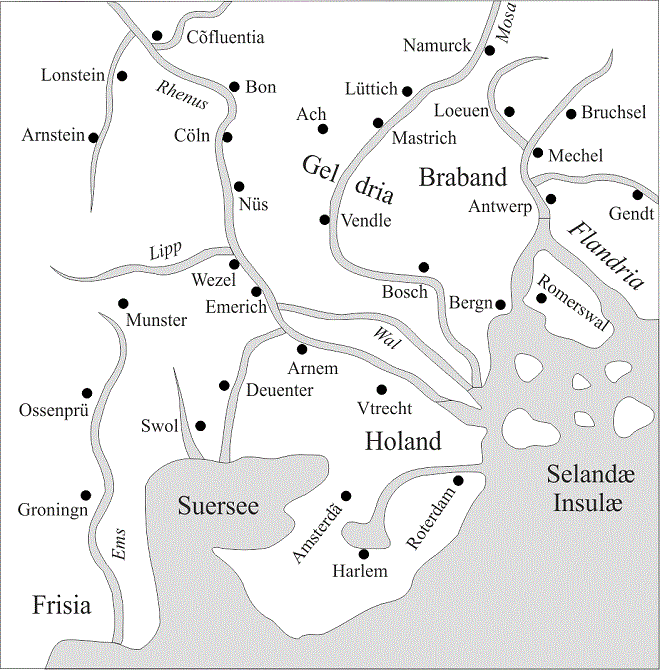
Afbeelding H4.3.2. Dat dergelijke schetsen slechts een zeer oppervlakkige gelijkenis met een moderne kaart hebben is geen reden om er neerbuigend over te doen. Ze werden gemaakt door mensen die nooit van hun leven een topografische kaart hadden gezien. En als zulke tekeningen door ons herkend worden als een bepaald deel van de wereld, dan wil dat zeggen dat de makers daarvan er een heel goed beeld van hadden. Welk beeld men in 1550 van Nederland had toont een kaart van Sebastian Münster (1489-1552), waarvan hier een stukje is nagetekend¹⁶. Het noorden ligt onder. Groningers storen zich aan het feit dat hun stad ten oosten van de Eems is terechtgekomen. Bijzonder aan het kaartje is de poging om plaatsen de namen te geven die ze in die tijd ook werkelijk hadden. Alleen bij Confluentia en Selandae Insulae heeft de auteur zich niet kunnen beheersen. Het was in die tijd heel gebruikelijk om plaatsnamen, in navolging van Ptolemaeus-uitgaven, Romeins te laten klinken. En men dacht toen dat het Latijn de taal van de Romeinen was.

Opmerkelijk is de aanwezigheid van “Romerswal” (Reimerswaal). Na de stormvloed van 5 november 1530 was de neergang van de stad al begonnen en in de loop van de tweede helft van de zestiende eeuw zou ze vervallen tot een eilandje met een paar huisjes. Door het kaartje 180° te draaien is te zien dat het werkelijk overeenkomsten heeft met een topografische kaart van Nederland. In dat geval ligt links onderaan Zeeland, dan de monding van de grote rivieren en de Hollandse kust, vervolgens de Zuiderzee en de Friese gebieden. Landinwaarts lijdt de kaart aan ernstige vervormingen. Toch is het knap dat iemand zonder de geografische kennis die wij hebben een dergelijke kaart kon schetsen. Natuurlijk kunnen er uit zo’n schets geen betrouwbare gegevens gehaald worden betreffende schaal, afstanden, kustlijnen etc.

Het is duidelijk dat Ptolemaeus over soortgelijke schetsen beschikte. Waarschijnlijk verschilden die onderling nogal in schaal en oriëntatie, voor zover men daar bij zulke tekeningen al van kan spreken, en is het zijn verdienste dat hij geprobeerd heeft om er één geheel van te maken. Na vergroten / verkleinen / roteren van de diverse delen heeft hij ze aan elkaar gepuzzeld en over het geheel een netwerk van meridianen en parallellen gelegd. Uiteraard bleven het daarna nog steeds schetsen, dat wil zeggen dat de coördinaten van de diverse plaatsen, rivieren en bergen niet gezien mogen worden als een nauwkeurige opgave van de lengte- en breedtegraden, maar hoofdzakelijk als een hulpmiddel om de plaats van de kaartonderdelen vast te leggen. Zodat voor het kopiëren niet de originele schetsen nodig zijn. Die kunnen aan de hand van de gevonden getallen min of meer gereconstrueerd worden.

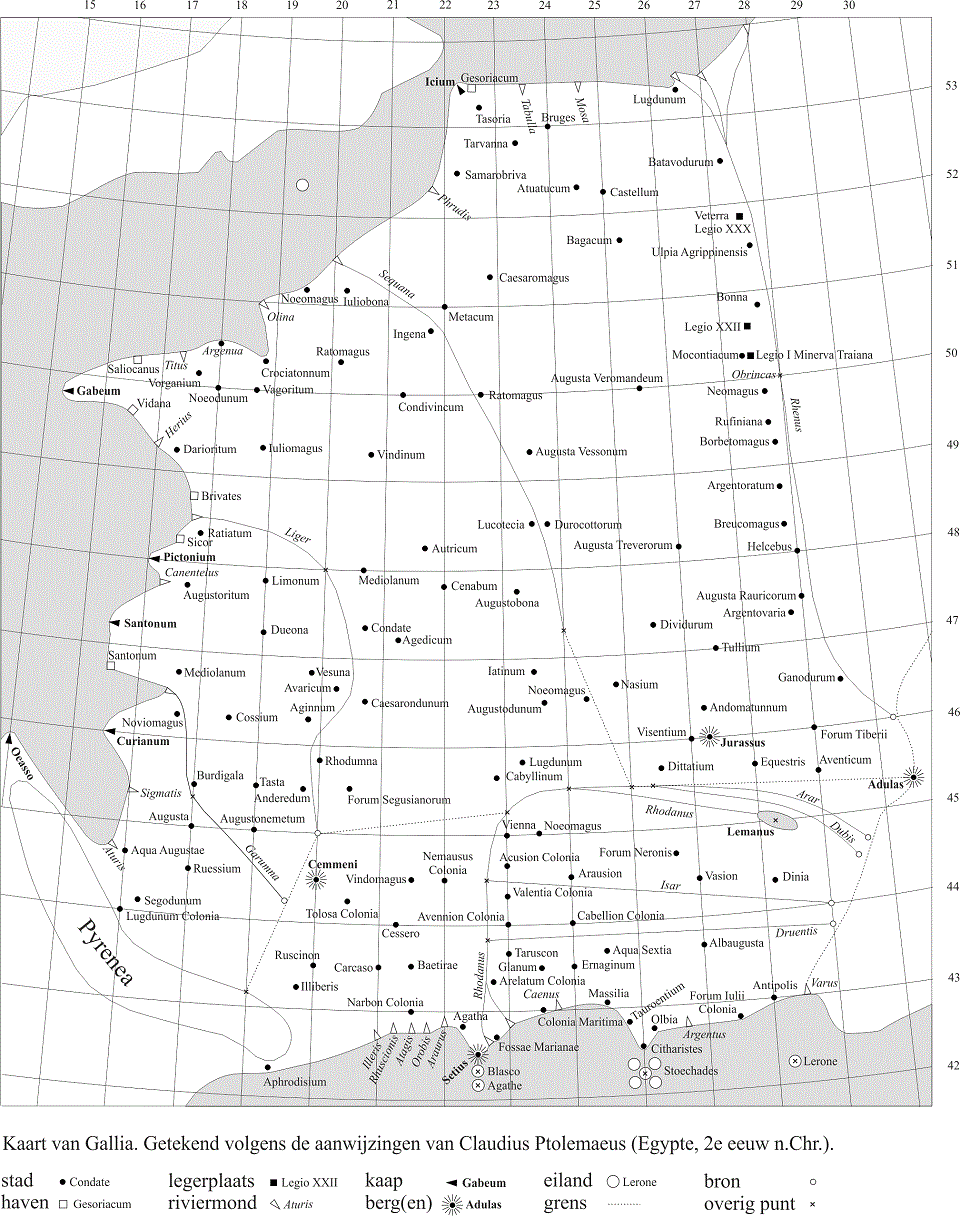
Afbeelding H4.3.3.(×) Doordat de door Ptolemaeus gebruikte begin- en eindpunten van zijn breedtegraden overeenkomen met die van ons (0° bij de evenaar, 90° bij de polen), hebben ze wel enig verband met de breedtegraden zoals wij die gebruiken, maar men moet daarbij dan niet op een graadje meer of minder kijken. De gesuggereerde nauwkeurigheid van 5’ is puur theoretisch. Als men werkelijk was gaan meten, dan was het misschien wel gelukt om de breedte van de diverse plaatsen met een dergelijke nauwkeurigheid vast te stellen, maar de juiste lengte van een plaats was in oudheid en middeleeuwen niet te bepalen. Pas sinds de uitvinding van de chronometer door John Harrison (1693-1776) kan men de lengte van een plaats vaststellen. Daarvoor waren er wel methoden die gebaseerd waren op kompasafwijkingen, sterbedekkingen door de maan, of de posities van de manen van Jupiter, maar ook die waren voor de stand van wetenschap en techniek in de oudheid te gecompliceerd. Bovendien, het is al opgemerkt, rekende Ptolemaeus per lengtegraad een afstand die 1½ keer te groot was. Het nulpunt van zijn lengtegraden lag ergens op de Kanarische eilanden. Omdat er in zijn tijd geen plaatsen bekend waren die westelijker lagen hoefde hij geen onderscheid te maken in ooster- en westerlengte. Al met al is er geen echte relatie te vinden tussen onze lengtegraden en die van hem. Maar dat is, gezien het feit dat zijn kaarten slechts grove schetsen zijn, ook niet van groot belang. Afbeelding H4.3.3.¹⁷ is zijn schets van Gallia.

Met enige goede wil kan men Gallia in de schets van Ptolemaeus wel herkennen. Dat betekent dat de maker daarvan er een vrij goed beeld van had. Het naar het westen uitspringende Bretagne is naar verhouding veel te klein getekend, terwijl de Gironde weer overdreven groot is. Wat hier wel een rol kan spelen is het feit dat de cartograaf de kustlijn niet duidelijk heeft aangegeven. Dat kon hij ook niet, want met behulp van coördinaten kunnen wel punten op de kaart aangegeven worden, maar om lijnvormige structuren, zoals rivieren en kustlijnen op die manier vast te leggen is ondoenlijk. We kunnen dus niet achterhalen hoe die er op de originelen hebben uitgezien. Zo lijkt ook Britannia op deze ‘kaart’ veel te mager, maar het is heel goed mogelijk dat de kustlijn ervan er op het origineel anders uitzag. Een aanwijzing daarvoor is de positie van het eiland Wight. Dat lijkt hier ergens tussen Britannia en Gallia midden in het Kanaal te liggen, maar men zal in de oudheid heus wel geweten hebben dat het zich vlak bij de Britse kust bevond. Van de rivieren heeft Ptolemaeus vaak alleen het begin- en eindpunt aangegeven. Hun verloop is dus ook vast anders dan op de originelen. Merk op dat de kust van Zuid-Frankrijk bijna twee maal zoveel lengtegraden beslaat als in werkelijkheid.

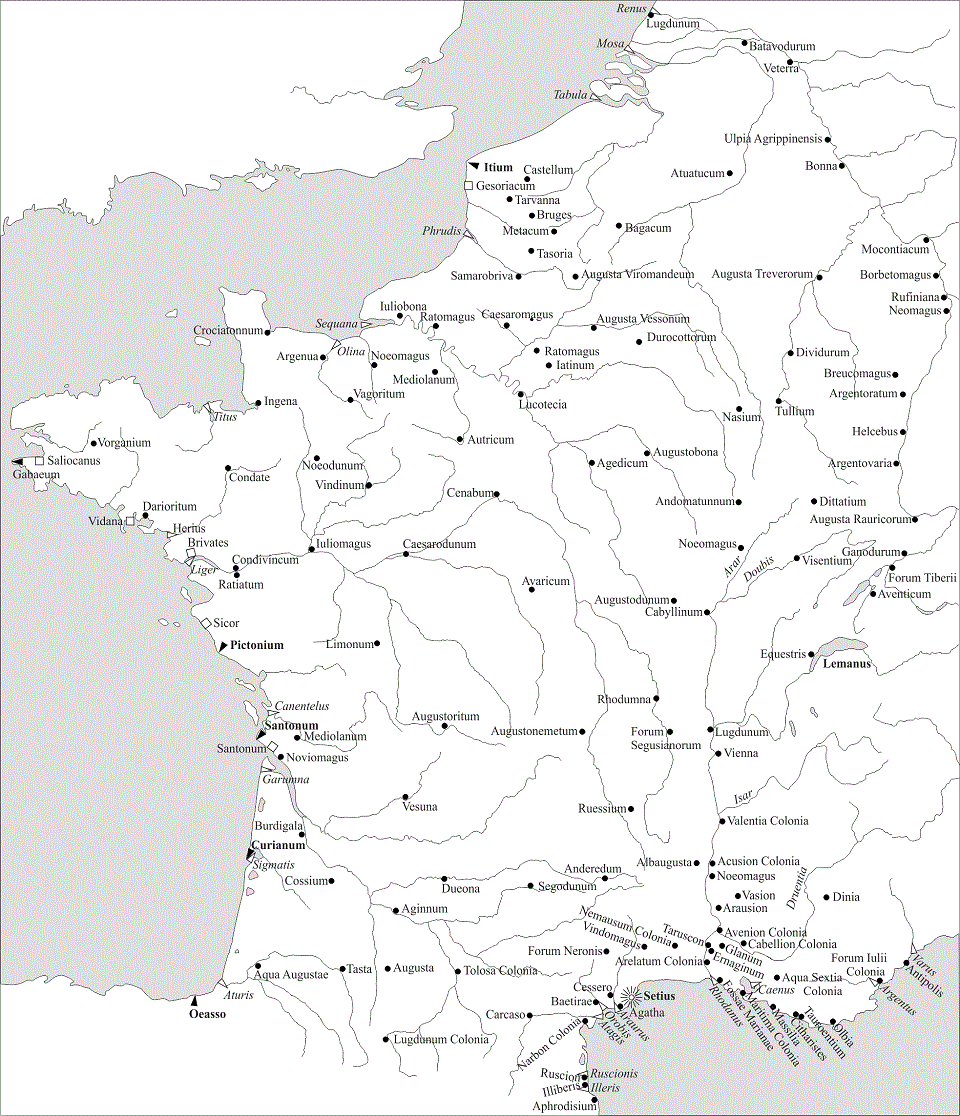
Afbeelding H4.3.4.(×) Hier zijn de door Ptolemaeus genoemde plaatsen neergezet op een moderne achtergrond. Er is daarbij geen rekening gehouden met de door hem genoemde coördinaten, want dan zou de kaart er heel anders uitzien. Afhankelijk van de formule waarmee men zijn westerlengte in die van ons zou omrekenen zou een deel van de plaatsen in zee en Britannia liggen, of ten oosten van de Rijn terechtkomen. Zijn breedtegraden zijn trouwens ook niet zonder meer te gebruiken. De lengte- en breedtegraden van Ptolemaeus zijn alleen maar een hulpmiddel om zijn kaarten te reconstrueren. De identificaties zijn niet allemaal zeker. Zo wordt Noeodunum (lengte 18, breedte 50) wel gelijkgesteld aan Jublains i.p.v. Sées. Op de kaart zijn de volgende identificaties aangenomen: bijlage.

De meeste van de door Ptolemaeus verzamelde gegevens zullen niet ouder zijn dan de regeringsperiode van Augustus (27 v.Chr.-14 n.Chr.). Namen als Augustodunum en Augusta Rauricorum wijzen daar op. De door hem vermelde plaatsen in ‘Groot Germania’ zullen zijn verzameld toen een verovering tot aan de Elbe op het programma stond. Mogelijk zijn de gegevens over de havens en rivieren aan de westkant van Gallia ouder. Misschien stammen ze uit de z.g. Periplus van Pseudo-Scylax. Een periplus is een rondvaart (Grieks περι = rondom en πλέω = varen). Het voorvoegsel pseudo (ψευδο) is trouwens ook Grieks en betekent vals, onwaar, gelogen. Het geschrift stamt uit de derde of vierde eeuw(?) v.Chr. en kan dus niet van Scylax zijn (6e eeuw v.Chr.). Als deze gegevens werkelijk zo oud zijn, dan moet men zich ook afvragen waarom Julius Caesar de grens van Aquitania bij de Garonne legde (H1.3), want ook bij Pseudo-Scylax strekt dat land zich uit tot aan de Loire. De gegevens van Pseudo-Scylax zijn trouwens in deze gids niet opgenomen. Ze verschillen alléén van die van Ptolemaeus doordat er afstanden in staan. Afstanden over zee wel te verstaan. En die zijn dermate onbetrouwbaar dat ze alleen voor verwarring en misverstanden kunnen zorgen. De kwestie van de afstanden over water komt nogmaals ter sprake bij het Itinerarium Maritimum in H7.3.

________________________________________